Minimum Distance Between Two Vectors . For this to be a minimum, taking partials,. Given a line l with equation and a point p not on l. I am able to work it out for the shortest distance from a vector to a point, but not from a vector to a vector. The scalar product of the direction vector, b, and the. The shortest distance from any point to a line will always be the perpendicular distance. The scalar product of the direction vector, b, and the. The distance between two lines is usually taken to mean the minimum distance, so this is the length of a line segment or the length. The distance \(d\) between points \((x_1,y_1,z_1)\) and \((x_2,y_2,z_2)\) is given by the formula. Given a line l with equation and a point p not on l. To find that distance first. The shortest distance from any point to a line will always be the perpendicular distance. The distance between two lines in $ \bbb r^3 $ is equal to the distance between parallel planes that contain these lines.
from www.reddit.com
Given a line l with equation and a point p not on l. The distance between two lines in $ \bbb r^3 $ is equal to the distance between parallel planes that contain these lines. The scalar product of the direction vector, b, and the. Given a line l with equation and a point p not on l. The shortest distance from any point to a line will always be the perpendicular distance. For this to be a minimum, taking partials,. To find that distance first. The distance \(d\) between points \((x_1,y_1,z_1)\) and \((x_2,y_2,z_2)\) is given by the formula. The distance between two lines is usually taken to mean the minimum distance, so this is the length of a line segment or the length. The shortest distance from any point to a line will always be the perpendicular distance.
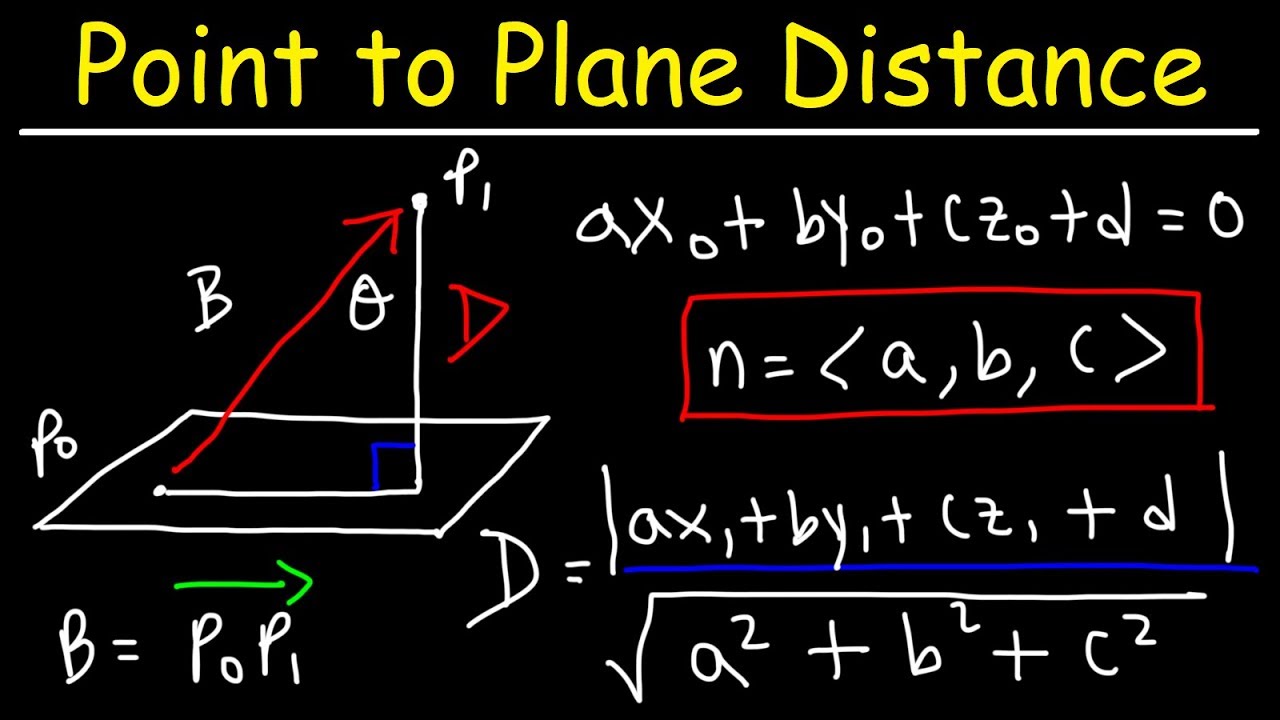
Calculate the distance from the point S( 3,7,4) to the plane 6x − 3y
Minimum Distance Between Two Vectors To find that distance first. The shortest distance from any point to a line will always be the perpendicular distance. I am able to work it out for the shortest distance from a vector to a point, but not from a vector to a vector. To find that distance first. The distance between two lines is usually taken to mean the minimum distance, so this is the length of a line segment or the length. The distance between two lines in $ \bbb r^3 $ is equal to the distance between parallel planes that contain these lines. For this to be a minimum, taking partials,. The shortest distance from any point to a line will always be the perpendicular distance. The distance \(d\) between points \((x_1,y_1,z_1)\) and \((x_2,y_2,z_2)\) is given by the formula. Given a line l with equation and a point p not on l. Given a line l with equation and a point p not on l. The scalar product of the direction vector, b, and the. The scalar product of the direction vector, b, and the.
From www.teachoo.com
Example 12 Class 12 Chapter 11 Find distance between lines Minimum Distance Between Two Vectors The distance between two lines is usually taken to mean the minimum distance, so this is the length of a line segment or the length. The distance between two lines in $ \bbb r^3 $ is equal to the distance between parallel planes that contain these lines. The distance \(d\) between points \((x_1,y_1,z_1)\) and \((x_2,y_2,z_2)\) is given by the formula.. Minimum Distance Between Two Vectors.
From www.youtube.com
Distance between two skew lines Vectors 2016 Test YouTube Minimum Distance Between Two Vectors The distance between two lines is usually taken to mean the minimum distance, so this is the length of a line segment or the length. For this to be a minimum, taking partials,. Given a line l with equation and a point p not on l. To find that distance first. I am able to work it out for the. Minimum Distance Between Two Vectors.
From www.teachoo.com
Find shortest distance between lines 3D Geometry (Vector, Cartesian) Minimum Distance Between Two Vectors The distance between two lines in $ \bbb r^3 $ is equal to the distance between parallel planes that contain these lines. The distance \(d\) between points \((x_1,y_1,z_1)\) and \((x_2,y_2,z_2)\) is given by the formula. The shortest distance from any point to a line will always be the perpendicular distance. The distance between two lines is usually taken to mean. Minimum Distance Between Two Vectors.
From www.teachoo.com
Find shortest distance between lines 3D Geometry (Vector, Cartesian) Minimum Distance Between Two Vectors For this to be a minimum, taking partials,. The distance between two lines is usually taken to mean the minimum distance, so this is the length of a line segment or the length. The distance \(d\) between points \((x_1,y_1,z_1)\) and \((x_2,y_2,z_2)\) is given by the formula. The distance between two lines in $ \bbb r^3 $ is equal to the. Minimum Distance Between Two Vectors.
From weaviate.io
Distance Metrics in Vector Search Weaviate Vector Database Minimum Distance Between Two Vectors For this to be a minimum, taking partials,. Given a line l with equation and a point p not on l. The scalar product of the direction vector, b, and the. The distance between two lines is usually taken to mean the minimum distance, so this is the length of a line segment or the length. The shortest distance from. Minimum Distance Between Two Vectors.
From cboard.cprogramming.com
distance between two vectors Minimum Distance Between Two Vectors The distance between two lines is usually taken to mean the minimum distance, so this is the length of a line segment or the length. The shortest distance from any point to a line will always be the perpendicular distance. Given a line l with equation and a point p not on l. The distance between two lines in $. Minimum Distance Between Two Vectors.
From www.nagwa.com
Question Video Finding the Distance between Two Parallel Lines Nagwa Minimum Distance Between Two Vectors To find that distance first. The shortest distance from any point to a line will always be the perpendicular distance. Given a line l with equation and a point p not on l. The scalar product of the direction vector, b, and the. The shortest distance from any point to a line will always be the perpendicular distance. The distance. Minimum Distance Between Two Vectors.
From www.youtube.com
Vectors Shortest Distance between Skew Lines ExamSolutions Maths Minimum Distance Between Two Vectors Given a line l with equation and a point p not on l. For this to be a minimum, taking partials,. The distance \(d\) between points \((x_1,y_1,z_1)\) and \((x_2,y_2,z_2)\) is given by the formula. I am able to work it out for the shortest distance from a vector to a point, but not from a vector to a vector. The. Minimum Distance Between Two Vectors.
From ca.finance.yahoo.com
Distance Formula Finding the Distance Between Two Points Minimum Distance Between Two Vectors The distance \(d\) between points \((x_1,y_1,z_1)\) and \((x_2,y_2,z_2)\) is given by the formula. Given a line l with equation and a point p not on l. For this to be a minimum, taking partials,. The shortest distance from any point to a line will always be the perpendicular distance. The distance between two lines in $ \bbb r^3 $ is. Minimum Distance Between Two Vectors.
From www.slideserve.com
PPT CHAPTER 5 INNER PRODUCT SPACES PowerPoint Presentation, free Minimum Distance Between Two Vectors The distance \(d\) between points \((x_1,y_1,z_1)\) and \((x_2,y_2,z_2)\) is given by the formula. The distance between two lines in $ \bbb r^3 $ is equal to the distance between parallel planes that contain these lines. The shortest distance from any point to a line will always be the perpendicular distance. The shortest distance from any point to a line will. Minimum Distance Between Two Vectors.
From www.youtube.com
Distance Between Two Vectors Example 1 YouTube Minimum Distance Between Two Vectors The distance between two lines in $ \bbb r^3 $ is equal to the distance between parallel planes that contain these lines. To find that distance first. I am able to work it out for the shortest distance from a vector to a point, but not from a vector to a vector. The distance between two lines is usually taken. Minimum Distance Between Two Vectors.
From mathsathome.com
How to Find the Vector Between Two Points Minimum Distance Between Two Vectors The distance between two lines is usually taken to mean the minimum distance, so this is the length of a line segment or the length. Given a line l with equation and a point p not on l. To find that distance first. Given a line l with equation and a point p not on l. The distance between two. Minimum Distance Between Two Vectors.
From mathsccw.weebly.com
Distance Between Two Points Mathsccw Minimum Distance Between Two Vectors For this to be a minimum, taking partials,. I am able to work it out for the shortest distance from a vector to a point, but not from a vector to a vector. The distance between two lines in $ \bbb r^3 $ is equal to the distance between parallel planes that contain these lines. To find that distance first.. Minimum Distance Between Two Vectors.
From www.youtube.com
Distance Between Two Vectors YouTube Minimum Distance Between Two Vectors Given a line l with equation and a point p not on l. The shortest distance from any point to a line will always be the perpendicular distance. For this to be a minimum, taking partials,. To find that distance first. Given a line l with equation and a point p not on l. The distance between two lines is. Minimum Distance Between Two Vectors.
From mathsathome.com
How to Find the Vector Between Two Points Minimum Distance Between Two Vectors The shortest distance from any point to a line will always be the perpendicular distance. For this to be a minimum, taking partials,. To find that distance first. Given a line l with equation and a point p not on l. The scalar product of the direction vector, b, and the. The distance \(d\) between points \((x_1,y_1,z_1)\) and \((x_2,y_2,z_2)\) is. Minimum Distance Between Two Vectors.
From www.youtube.com
How to find the shortest distance between points on lines Vectors in Minimum Distance Between Two Vectors For this to be a minimum, taking partials,. I am able to work it out for the shortest distance from a vector to a point, but not from a vector to a vector. Given a line l with equation and a point p not on l. The shortest distance from any point to a line will always be the perpendicular. Minimum Distance Between Two Vectors.
From medium.com
Unlocking Insights Understanding Vector Similarity in Machine Learning Minimum Distance Between Two Vectors The distance \(d\) between points \((x_1,y_1,z_1)\) and \((x_2,y_2,z_2)\) is given by the formula. The scalar product of the direction vector, b, and the. To find that distance first. Given a line l with equation and a point p not on l. The shortest distance from any point to a line will always be the perpendicular distance. The scalar product of. Minimum Distance Between Two Vectors.
From www.youtube.com
Vectors Closest point / Shortest distance to a line ExamSolutions Minimum Distance Between Two Vectors For this to be a minimum, taking partials,. The distance between two lines is usually taken to mean the minimum distance, so this is the length of a line segment or the length. Given a line l with equation and a point p not on l. The shortest distance from any point to a line will always be the perpendicular. Minimum Distance Between Two Vectors.